حياة رقمية (الحساب الثنائي)

التفاصيل

تم إنشاءه بتاريخ الأربعاء, 21 أيلول/سبتمبر 2022 09:07

كتب بواسطة: المهندس أحمد فخري

               حياة رقمية(الحساب الثنائي)

في هذه السلسلة من المقالات ساقوم بتغطية شاملة لجميع ما يتعلق بالتقنيات الرقمية الجديدة والتي تشمل: الحواسيب، الهواتف الذكية، الذاكرات بانواعها، البرمجيات، التطور العلمي للمخترعات الحديثة، انظمة البث والانترنيت باجيالها، الاجهزة التي تعمل على البطاريات كالسيارات الحديثة بشقيها الكهربائية والهجين، البطاريات القابلة للشحن، اجزاء الكومبيوتر، وسائل تخزين المعلومات من السحابات والاقراص المدمجة واصابع الفلاش، ونظام البلوتوث والوايفاي. كما ساقوم ايضاً بشرح طرق اختيار الحواسيب الجديدة وكيفية المقارنة بين مواصفات واحدة بالاخرى. وهذا ينطبق على الهواتف الذكية ايضاً. ساتطرق كذلك في مقالات لاحقة الى البرمجيات وانواعها وكيفية انتقائها لتناسب انظمة تشغيل متعددة. وما هي بروتوكولات الاتصال بالحاسوب؟
بالاضافة الى شرح مبسط للكثير من الامور التي تطرأ على مسامعكم هذه الايام وتتسائلون عنها وعن كيفية استعمالها وتشغيلها. ارجو من القدير العزيز ان يمكنني من توصيل كل ذلك للقارئ الكريم.
الحساب الثنائي binary arithmetic
اول موضوع ابدأ به هذه السلسلة من المقالات هو الحساب الثنائي لان جميع الحواسيب تستند عليه وكلمة (الرقمية) مأخوذة منه. ولكي نتمكن من التعامل مع الحواسيب او (الكومبيوتر)، يجب علينا ان نفكر كما تفكر الحواسيب. ونمط رياضياتها يستند الى الحساب الثنائي. كان اجدادنا الاولون يستعملون النظام الاثني عشري (الدزينة او الدرزن) بحسابهم بحيث اصبح ذلك يتجسد بكل شيء من تعاملاتهم التجارية وعدد اشهر السنة مروراً بـالآلهة التي اخترعوها الاغريق واليونانيين للعبادة وحتى المعتقدات الحديثة. بقيت آثآر الدزينة حاضرة اليوم بالكثير من اللغات العالمية. فبالانكليزية مثلاً الدزينة او dozen لا تزال مستعملة حتى يومنا هذا ولكن ربما بسياق الحديث فقط وليس بالمواد العلمية. فالانكليز عندما يريدون ان يرمزوا الى بعض الرجال يقولون half a dozen men اي نصف دزينة رجال. وعندما يريدون ان يقللوا من عدد معين يقولون A few dozen اي بعض من الدزينات. اما بالفرنسي فالرقم 12 هو Douze والاسبانية doce والبرتغالية doze والرومانية doisprezece واليونانية dódeka...الخ
اما نظام الحساب اللاتيني فبالرغم من عراقته والذي كان لا يخدم التطور العلمي لصعوبة ترقيمه فالجميع يعلم انه يبدأ ب I II III IV V VI حتي يصل الى الرقم 10 الممثل بـ (X). تخيل ان الرقم العشري 1112 يساوي MCXII. امر محير حقاً اليس كذلك؟.
بقي العلماء القدامى يستعملون ذلك النظام لفترة غير قليلة حتى صار الناس يتفحصون اصابعهم ليجدونها عشرة ويتبينون ان العد على الاصابع سيكون اسهل من العد بنظام الدزينة او الترقيم الحرفي باللاتينية. لذا اصبح الانتقال اليها امراً تدريجياً لانه اكثر منطقياً. اذكر ان بريطانيا وحتى عام 1970 كانت تستعمل بعض منها في عملتهم النقدية إذ ان الجنيه الاسترليني كان فيه 20 شلناً والشلن الواحد يحتوي على (12) بنساً. بقيوا على هذا المنوال حتى دخلت عليهم الرقمنة (digitization) عندما حولوا عملتهم الى اجزاء عشرية بدلاً من الرقم 12. فاصبح الجنيه يشمل 100 ﭕنساً. بعض الامور بقيت على حالها لاسباب غير معروفة تماماً. ففي حساب الوزن والمسافة ببريطانيا وامريكا لاتزالان تستعملان الرطل بالوزن والميل للمسافة وبعض من الدول الاخرى. اما الطيران فانقسموا الى قسمين: البعض يستعمل (القدم) للارتفاع والبعض يستعمل المتر فتسمع طياراً يقول ان الطائرة بلغت 30000 قدم وآخر يقو ارتفعت الى 10000 متر.
بعد تلك الحقبة صار باقي العالم كله يستعمل الارقام العشرية بكل مجالات الحياة بدءاً بالمسافة المترية وصولاً الى الحواسيب. لكن العلماء الاولون الذين سعوا لاستعمال الارقام وجدوا ان تمثيل الارقام العشرية بشكل كهربائي امراً صعباً جداً. لذلك قاموا باستنباط نظام الحساب الثنائي. وهذا النظام على الشكل التالي.:
الرقم 0 يقابله الرقم 0 بالثنائي
الرقم 1 يقابله الرقم 1 بالثنائي
الرقم 2 يقابله الرقم 10 بالثنائي
الرقم 3 يقابله الرقم 11 بالثنائي
الرقم 4 يقابله الرقم 100 بالثنائي
الرقم 5 يقابله الرقم 101 بالثنائي
الرقم 6 يقابله الرقم 110 بالثنائي
الرقم 7 يقابله الرقم 111 بالثنائي
الرقم 8 يقابله الرقم 1000 بالثنائي
الرقم 9 يقابله الرقم 1001 بالثنائي
الرقم 10 يقابله الرقم 1010 بالثنائي
وهكذا دواليك. اي ان الرقم الثنائي يكون عبارة عن سلسلة من الاحاد والاصفار تمثل اي رقم عشري في الطبيعة. والسؤال المطروح هنا: كيف سيساعدنا هذا التمثيل في فهم للنظام الرقمي؟ وكيف سننقل المعلومات من خلالها؟
والجواب على ذلك بسيط جداً. فلو فرضنا ان لدينا دارة كهربائية غير معقدة كالتالي:
نقوم بربط مصباح نور صغير بالاسلاك مع بطارية. ونضع مفتاحاً في الوسط كما هو مبين بالشكل (1). فعندما يكون المفتاح مرفوعاً الى الاعلى تكون الدارة غير مكتملة فيكون الضوء قاتماً اي لا يعمل. وإذا ما قمنا بغلق المفتاح اي اكملنا الدارة فإن التيار الكهربائي بسالبه وموجبه سيصلان الى المصباح فيضيء.

                                       

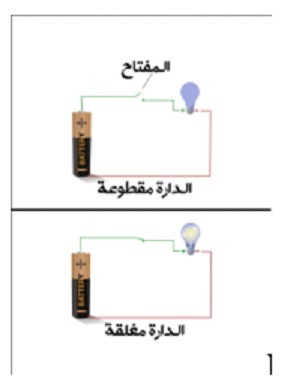
الشكل (1)
اعتقد انها جداً بدائية وسهلة الفهم على الجميع اليس كذلك؟
اذا اعتبرنا ان حالة الضوء المطفئ هي صفر (0). لذا فأن الضوء المشع هي (1)
كيف نستطيع ان ننقل المعلومات من خلال هذه الدارة؟
دعنا نختلق قصة معينة لتبسيط هذه النظرية:
جاء صديقك لزيارتك مع زوجته وابنته الصغيرة ذات العشر سنوات. قمت انت بواجب الضيافة وقدمت لهم وليمة دسمة. بعد الانتهاء من الطعام خرجت زوجة صديقك وابنتها مع زوجتك ليجلسا في الحديقة فسألت انت صاحبك،
انت : الا زلت مقلعاً عن التدخين؟
الصديق : كلا ولكني كذبت على زوجتي وقلت لها انني ما زلت لا ادخن.
انت : هل تريد ان تدخن لفافة الآن؟ فانا ليس لدي اي اعتراض على تدخينك.
الصديق : اجل ولكن، ماذا لو دخلت علينا زوجتي فجأة ووجدتني ادخن؟
هنا تضع المصباح الكهربائي بجانبه لكنك تستعمل سلكاً طويلاً يصل الى الشباك وتربطه بالمفتاح (سويچ). تجلس انت بجانب الشباك وتراقب الموقف وتقول له: أذا كان الضوء قاتماً فان بامكانك التدخين. اما إذا توهج الضوء فهذه دلالة على ان زوجتك قادمة. وبتلك الحالة تطفئ لفافتك.
اي انك استطعت ان تنقل له من خلال تلك الدارة الكهربائية معلومتان. اما ان:
1 زوجته لا تزال بالحديقة (0).
2 زوجته قادمة (1).
لكن ذلك النظام سيكون محدوداً لانك تنقل مجرد معلومتان فقط من خلال دارة كهربائية واحدة. ولان الدارة الواحدة تسمة BIT بت.
ماذا لو ضاعفنا الدارات اي اننا نربط مصباحين وبطاريتين

                        

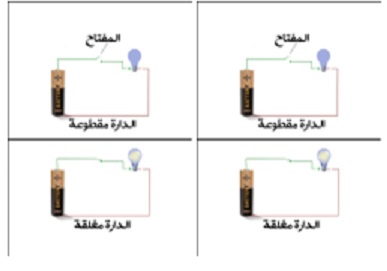
بهذه الحالة بامكانك ان توصل لصديقك اربعة معلومات كما في الجدول التالي:

                                          

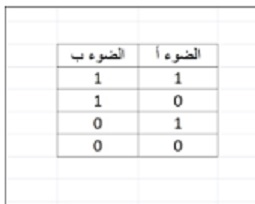
لنفرض ان الضوء (أ) يرمز الى زوجة الضيف والضوء (ب) يرمز الى زوجتك فبامكاننا ان تنقل اربعة معلومات الى الضيف من خلال المصابيح الآن:
زوجة الضيف قادمة مع زوجتك (1 و 1)
زوجة الضيف قادمة وحدها (1 و 0)
زوجتك قادمة وحدها (0 و 1)
الزوجتان لا تزالان بالحديقة (0 و 0)
هذا يعني باستخام دارتان تمكنا من نقل اربعة معلومات. وباضافة دارة ثالثة يصبح لدينا ثمان احتمالات كالتالي:

                                     

ليس هناك حد اقصى لكمية الاضواء المستعملة. لذلك فإن كل ضوء من هذه الاضواء سيحمل القيمة 1 او 0 ويسمى بت (BIT).
اما اذا كان لدينا 8 مصابيح فبهذه الحالة سيصبح اسمها بايت (BYTE). وهي الوحدة الصغرى بداخل الكومبيوتر.
بما اننا نقيس المسافات بالمليمتر والمتر والسنتمتر. ونقيس الوزن بالغرام والكيلوغرام والطن. فاننا نقيس كمية المعلومات بالبايت والكيلو بايت كالتالي:
1 كيلوبايت يساوي الف بايت KB
1 ميغا بايت يساوي مليون بايت MB
1 گيگا بايت يساوي بليون بايت GB
1 تيرا بايت يساوي ترليون بايت TB
1 ﭘيتا بايت يساوي الف ترليون بايت PB
وهكذا دواليك.
بقي ان انوه الى ان بعض الحواسيب يكون حجم الكلمة فيها 32 بت اي 4 بايتات لكلمة الواحدة لان 32 تقسيم 8 هو 4. والبعض 64 بت اي 8 بايتات. وكلمة الكومبيوتر بالامكان تخيلها كحرف بشري واحد كأن يكون حرف الالف او الحاء او الميم او الدال. لذا فإن كتاب رقمي كامل يحتوي على 200 صفحة قد يشغل حيز 700 كيلو بايت. نفس ذلك الكتاب اذا احتوى على صور ذات وضوح عال قد يشغل حيز 90000 كيلو بايت. سنتحدث بدروس لاحقة عن وسائل التخزين في الذاكرة وفي الاقراص بجميع انواعها الفيزيائية وغير الفيزيائية.
وبهذا اكتفي بهذا القدر من المعلومات عن الحساب الثنائي وساقوم بالتطرق الى موضوع آخر متعلق بالحياة الرقمية في الحلقة القادمة. تابعونا...